――相対性理論によると運動している時計は進み方が遅くなるといいますよね。それに関連したものとして「ウラシマ効果」というのをよく耳にしますが、これはどういった現象なんですか。
ウラシマ効果というのは、「時空」を移動するときの道のりは直線ルートよりも遠回りした方が短くなり、その結果、経過時間も短くなるという現象です。有名なのは「双子のパラドックス」というたとえ話です。
アリスとボブという20歳の双子がいたとして、そのうちのボブだけが光速の80%で飛行する宇宙船に乗り、地球から4光年先にあるアルファ・ケンタウリという星をめざすという状況を考えます。
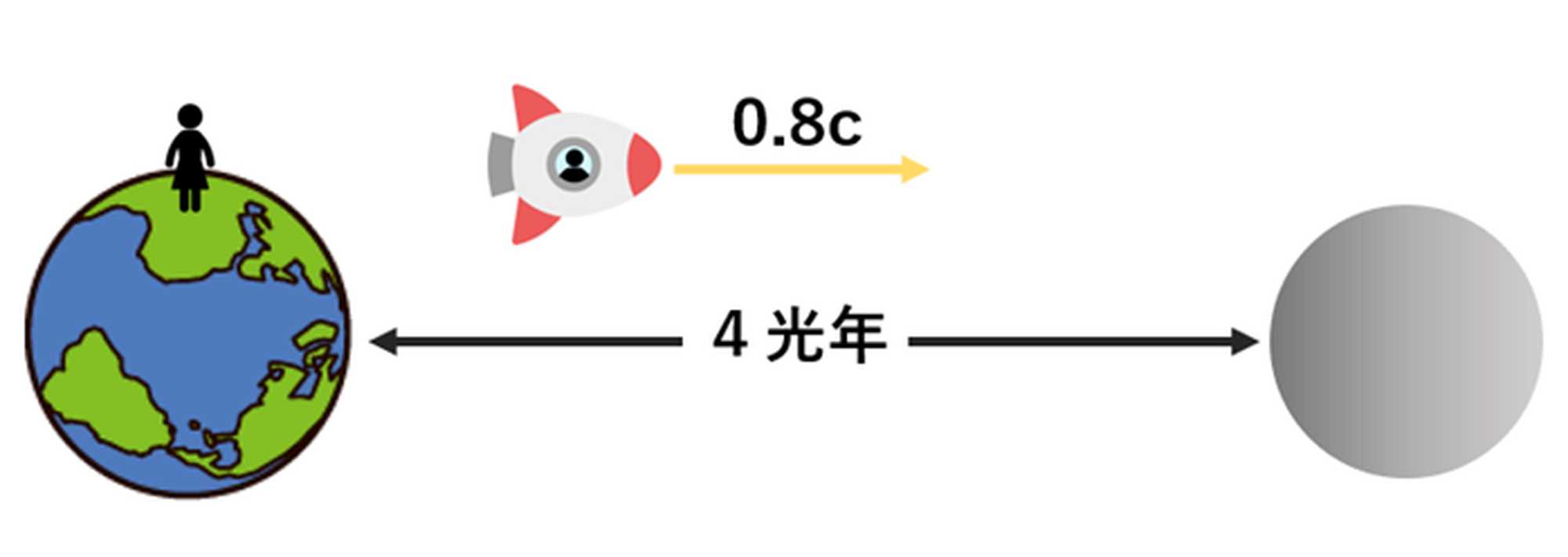
4光年の距離を光速の80%(0.8c)で飛ぶので、地球にいるアリスから見ると、宇宙船がアルファ・ケンタウリに到着するのは5年後です。しかしそのとき、宇宙船に乗っているボブの時間はなぜか3年しか経過していない。その後、宇宙船が地球に帰ってきて二人が再会すると、ボブは26歳なのにアリスは既に30歳になっていた、といった話です。
――双子なのに年の差ができてしまったと。なぜそんなことが起きるんですか?
まずボブについて見ていきましょう。宇宙船が光速の80%で飛んでいるということは、その中にいるボブから見ると、(宇宙船は止まっていて)地球とアルファ・ケンタウリが光速の80%で移動していることになります。するとローレンツ収縮(光速に近い速度で運動すると、その物体の長さが固有値よりも短くなる現象)が起こり、地球とアルファ・ケンタウリの距離が4光年から2.4光年に変化するんです。この2.4光年の距離を0.8c(cは光速)で移動するので、3年で到着するわけです。
「運動する時計は遅れる」という言い方がよくされますが、これは相対的に静止している観測者(アリス)の視点によるもので、宇宙船に乗っているボブから見ると、時計は地球にいるときと同じように動いています。つまりボブにしてみると、時間がゆっくり流れたから本来は5年かかるところを3年で着いたのではなく、地球とアルファ・ケンタウリの距離が短くなったから早く着いたんです。
一方、地球にいるアリスから見るとアルファ・ケンタウリまでの距離は4光年のままなので、宇宙船のなかの時間の進み方が遅くなったと感じられるわけです。
――本来は5年かかるところを3年で着いたという現象の認識は同じでも、それが空間の効果によるものなのか、時間の効果によるものなのかは観測者によって異なるんですね。
その根本にあるのは、宇宙は時間と空間が一体化した「時空の幾何学」によって構成されているということです。二次元空間で点の位置を特定するにはX座標とY座標が必要なのと同じく、宇宙における運動は空間軸と時間軸がなければ表せません。ただし、上の例からもわかる通り、宇宙は変化することのない「絶対空間」ではないし、全宇宙を一様に流れる「絶対時間」なるものも存在しない。そのため、宇宙の物理現象は常に、観測者によって異なる時空の枠組みのなかで見ていく必要があるわけです。
時空の幾何学は空間だけの世界の幾何学(ユークリッド幾何学)とは大きく異なります。地球上で、たとえばどこかに出かけるとたら、現在地と目的地を結んだ直線が最短の道のりですよね。ユークリッド幾何学ではこのように、ある2点間の距離はその2点を直線で結んだときに最短となるのですが、時空の幾何学では遠回りした方が道のりが短くなる。これは、前回お話したように、時間と空間を併せた世界では直角三角形の斜辺の2乗が、直角をはさむ両辺の2乗の差になることが理由です。
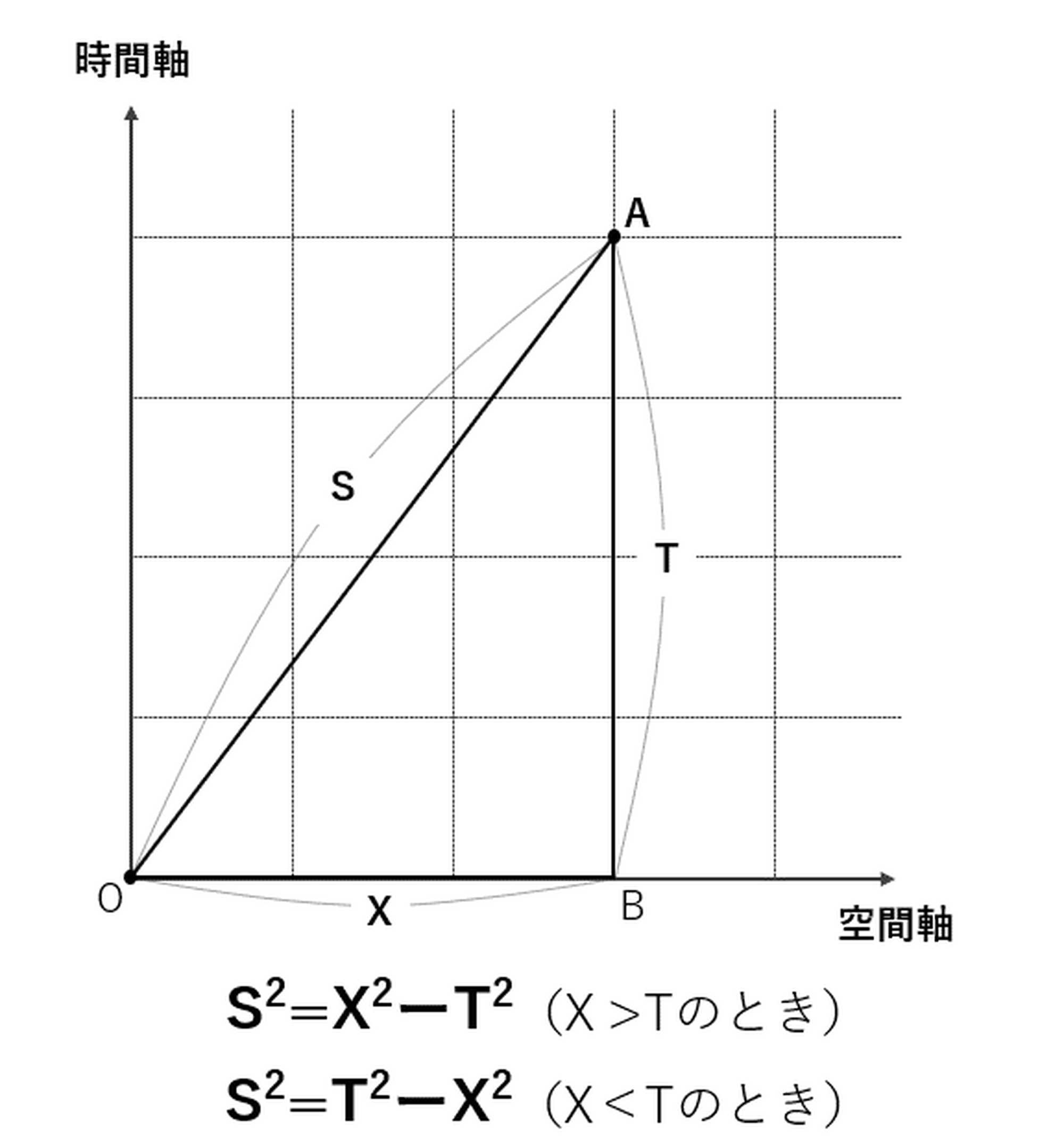
――上の図でいうと、原点Oから直接Aに行くより、O→B、B→Aというルートを辿る方が、道のりが短くなるわけですね。
そういうことです。ただ、無時間で移動することはできないので、この図のO→Bというルートは現実には成立しませんが。これらを踏まえて双子のパラドックスをアリスの視点から図示すると、以下のようなります[図2]。
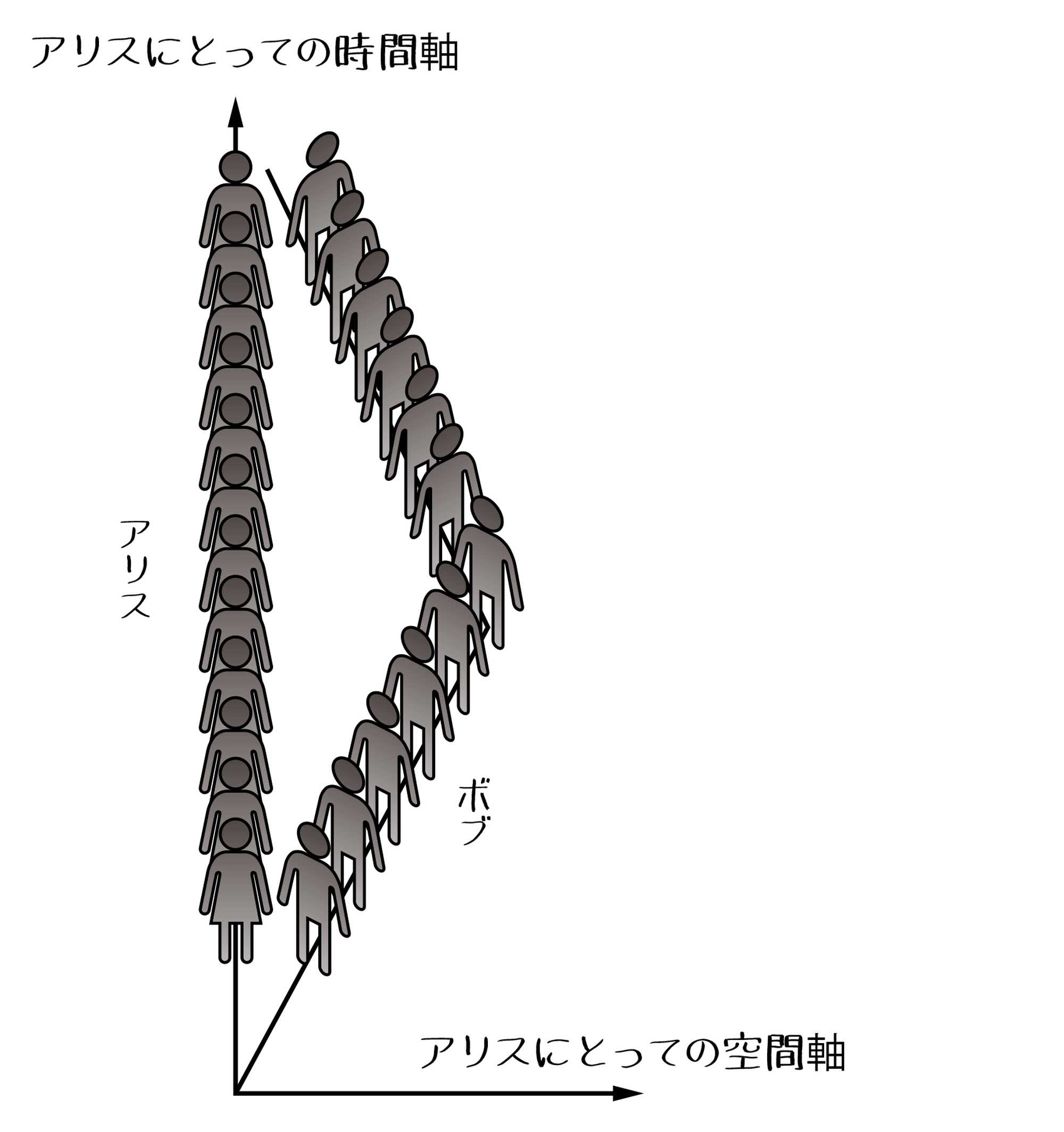
――ずっと地球にいるアリスより、アルファ・ケンタウリに寄り道したボブの方が、道のり(経過時間)が短くなるわけですね。
光速とは何か
――いまの例でもそうですが、物理学では光の速さというのがよく出てきますよね。数ある物質や物理現象のなかで光だけが特別視されるのはなぜなんですか?
「光速」というのは質量がゼロのものが進む最高速度であって、実は光に限った速さではありません。ただ、質量がゼロでかつ遠方まで伝播していくものが光だけなんですよ。たとえば、原子核の中にあるグルーオンという粒子も質量がゼロなので、もしも遠方まで飛んでいくことができたら光速(c)で進むのですが、グルーオンはほとんどが原子核の中にとどまっているので観測できない。観測できる唯一のものが光なのでアインシュタインも光を相対性理論のベースに据えていますが、別に物理学者が光だけを特別なものとみているわけではありません。
――光よりもむしろ「光速」の方が重要だったんですね。
たとえば長さの単位をどうやって決めているかってご存知ですか。
――昔はメートル原器(編注:メートル法の国際化のために1879年に制作された合金製の物差し。子午線の4千万分の1になるように調整された)を使っていたというのは聞いたことがあります。
おっしゃる通り以前はメートル原器で決めていましたが、現在では光が真空中を299,792,458分の1秒の間に伝わる距離を1メートルと定義しています。つまり「光速」というのは、時間の長さを空間の長さに換算するための係数なんです。なぜそんなことをするかというと、時間と空間は一体となって「時空」という枠組みを形成するので、両者の長さの尺度をあわせる必要があるんです。
いま最も精密に測定できる物理量は時間です。原子時計を使うと時間はかなり厳密に計れるので、これによってまずは「1秒」というものを定義する。現在では、セシウム原子に吸収されるマイクロ波が9,192,631,770回振動するのにかかる時間が1秒です。この1秒と「光速」を用いて1メートルを決めているわけです。
つまり「光速」というのは実際に光が飛ぶ速さというより、時間と空間の換算係数といった意味合いの方が強い。実は光の速度が「光速」ではないという物理学理論はけっこうあり――こう言うとややこしいので「光速」をcとすると――、相対性理論の枠内でも光がcよりも遅くなるという理論をつくることは可能です。
――それは面白いですね! 逆にcより速くなるということはあり得ないんですか?
それはちょっと難しい問題ですが、相対性理論に適合するように方程式をたてると、伝播速度がcを超えて変化するときにその方程式が破綻するんですよ。この世界は数式で記述できるというのが物理学の信念であり、数式にできない現象はあり得ないということで「cは超えられない」ということになっていますが、本当にそうかと言われるとわからないというのが正直なところです。
――相対性理論の方程式といえばE=mc2がよく知られていますよね。Eはエネルギーでmは質量なので、cを単なる係数だとするなら、この式が意味するのはエネルギーと質量は等価であるということですか。
そういうことです。この式は特殊相対論の中に出てくるのですが、アインシュタインがニュートンの運動方程式を特殊相対論に適合するように書いてみたところ、エネルギーの項のところに質量の項があらわれたので、この式を導いたようです。ただ、その時点ではE=mc2の本当の意味はよくわかっていなかったんじゃないかと思います。
――とおっしゃいますと?
特殊相対性理論が出てから13年後の1918年に、エミー・ネーター(1882-1935)というドイツの数学者が「ネーターの定理」を公表し、それによってエネルギーとは何かということが明確になりました(彼女の議論はエネルギーに限らずもっと一般的ものですが)。それによると、エネルギーは、「時間とともに物理法則が変化しないならば、保存する量」と定義されます。ちょっとわかりづらいかもしれませんが、重要なのは、この定義を使うと質量という概念がいらなくなるということです。
昔はエネルギーと質量は別のものだと考えられていました。さらに質量を慣性質量と重力質量にわけてなんだかよくわからないことになっていたのですが、これらをエネルギーで統一して議論できるようになったんです。
このことは次回もお話しますが、電子や陽子といった粒子の質量とは、そこに閉じ込められているエネルギーの量に他なりません。そのエネルギーの元を辿ると、行き着くのはビッグバンです。要するに、今あるすべての物質は、ビッグバンのときに解放されたエネルギーが、宇宙の膨張とともに希薄化されることなく、共鳴状態を維持しているものなのです。


