――地球が太陽のまわりを回っているのは常識中の常識ですが、知識としては知っていても、われわれが日常生活でその地球の動きを感じることはありません。そのことが、天動説が長年信じられていた主な理由だと思うんですけど、私たちが地球の公転運動に気づかない、気づけないのはなぜなんでしょうか。
物理学的にいうと、動いているか止まっているかを決定する物理法則は存在しないから、ということになります――これを「相対性原理」といいます――。等速運動している乗り物の中で手からリンゴを落とすと、リンゴは(地面に立っているときと同じく)垂直に落下する。この現象自体はガリレオの時代から知られていましたが、ニュートンの運動方程式によってそれが理論的に裏付けられました。つまり、ニュートンの運動方程式には、等速運動をしている座標系と静止している座標系では力学現象が同じになることが表されているのです
これと同じようなアプローチで考えたのがヘンドリック・ローレンツ(1853-1928)です。ローレンツは電磁気現象を記述する「マクスウェル方程式」を変形し、どちらの座標系でも同じ結果を導くことを証明しました。つまり、(マクスウェル方程式が正しいとすれば)電磁気学においても地球が動いているか止まっているかを判断することはできないというわけです。
――物理現象を記述する基本的な方程式が変わらないから、地球が動いていることは観測できないんだと。
そういうことです。しかし、アインシュタインはこれに異を唱えました。力学と電磁気学は――最終的には素粒子物理学などで統一できるのかもしれませんが――、彼の時代にはまったく異なるものだと見なされていました。にもかかわらず、なぜ、そのどちらでも、地球が動いているか止まっているかを観測できないのか。アインシュタインはそれが不思議だったようです。
それに、電磁気学のなかだけでも、異なる物理現象であるはずなのに、なぜか同じ結果になるということがあります。磁石とコイルを使った起電力の実験がそのひとつです。
コイルを固定してそのなかに棒磁石を挿入すると、ファラデーの「電磁誘導の法則」によってコイルに誘導起電力が発生します。次に、棒磁石を固定してコイルの方を動かすと、今度はフレミングの「左手の法則」に従って電子が力を受け、やはり起電力が生じる。
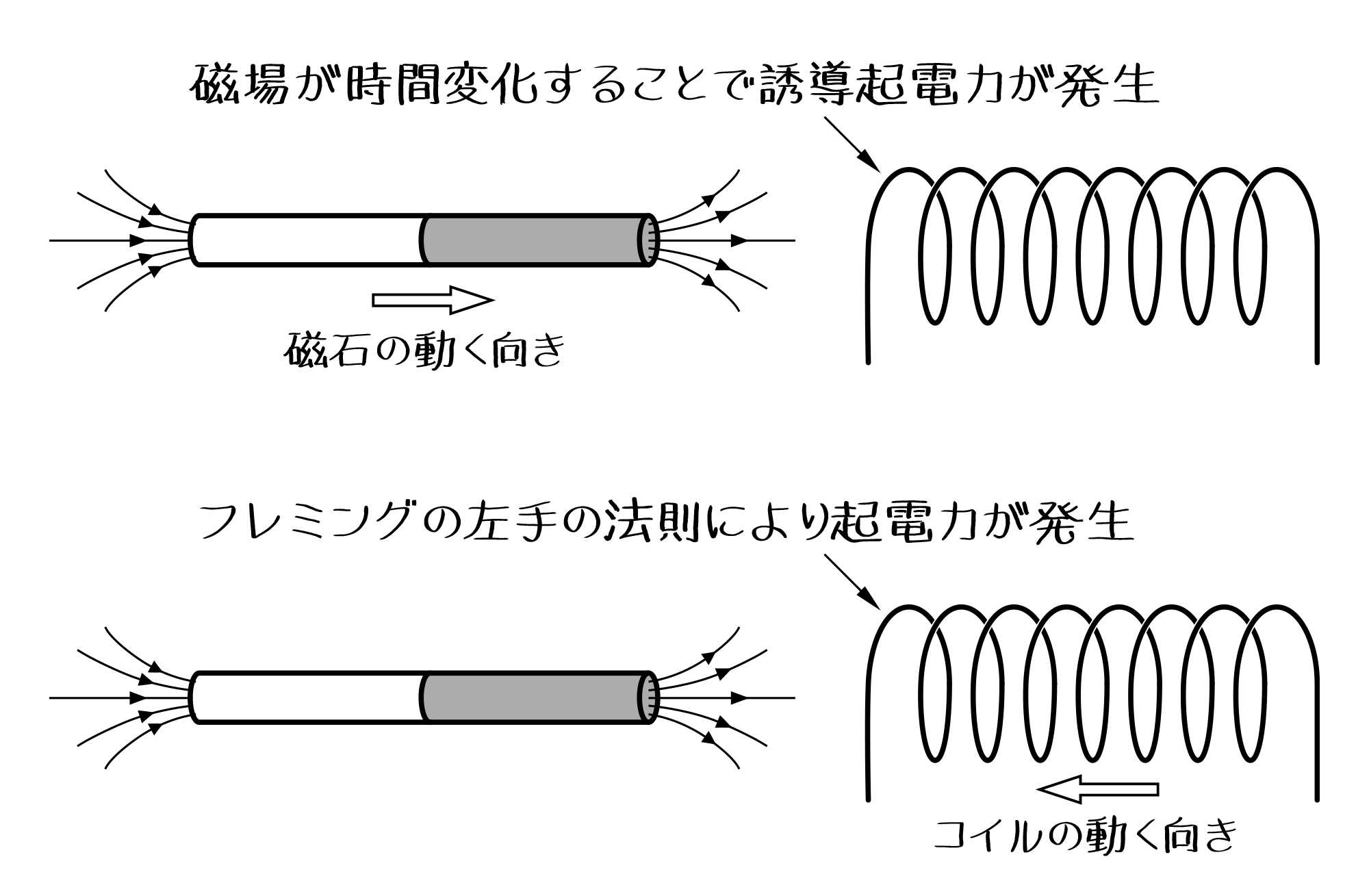
この二つの現象は物理学的には異なるものなのですが、コイルと磁石の相対速度が同じであれば、起電力の数値はまったく同じになります。そのことがアインシュタインにはものすごく不思議だった。ちなみに、ここで磁石を地球に、コイルを太陽に置き換えると、この実験はそのまま地球が動いているのか太陽が動いているのかが判断できないという話になるのがわかると思います。
――起電力の数値が同じなので、磁石(地球)が止まっていてコイル(太陽)が動いているのか、その逆なのかがわからないわけですね。
この問題に対してアインシュタインの出した答えが、冒頭に挙げた「相対性原理」です。地球の公転運動が観測できないのは、ローレンツの言うように方程式が同じになるからではなく、自然界の原理によるものだと。つまり、この宇宙にはニュートンの考えた「絶対空間」のような静止系は存在せず、何が動いていて何が止まっているかは常に相対的に語ることしかできないというわけです。
その後、核物理における原子核の現象や素粒子論においても同じことが言えると判明し、アインシュタインの考えが正しかったことが改めて確認されました。その時には既に相対論の正しさが広く知れ渡っていたので科学者たちは驚きませんでしたが、どんな物理現象を調べても、動いていることと止まっていることの区別がつかないということは、やはり驚くべきことですよね。
――地動説もそうだったと思いますが、新しい発見というのはやはり、常識的な感覚にとらわれない発想からが生まれるんですね。
時空の幾何学
ただ、「特殊相対性理論」を発表した1905年時点のアインシュタインは、相対性原理の真の意味まではわかっていなかったと思います。それを明らかにしたのは、学生時代のアインシュタインを教えたこともあったミンコフスキーという数学者です。
大学でのアインシュタインは成績がぱっとせず教授たちの覚えも悪かったようですが、その「劣等生」がすごい論文を発表したというので、ミンコフスキーもきっと本気になって「特殊相対性理論」を読み、相対性原理が何を意味しているのかを考えたのでしょう。
ミンコフスキーは、相対性原理とはこの世界の基になっている幾何学の問題だと考えました。そこで出てくるのが「時空」という概念です。つまり彼は、時間と空間を一体化させて、「時空の幾何学」を完成させたんです。
――「時空」という言葉自体はよく聞きますけど、それまでの時間や空間の考え方とは何が違うんですか。
たとえば運動というのは、ある物体が時間の経過とともに空間のなかを動くことだ、というのが従来の考え方なんですけど、ミンコフスキーはそれを否定します。時間と空間とは一体化していて切り離せない「時空」であり、あらゆる物理現象はその時空という枠組みのなかで起きる。つまりこの宇宙は「時空の幾何学」によって構成されているのだ。そのように考えると、運動というのは時空の中の線分だということになります。
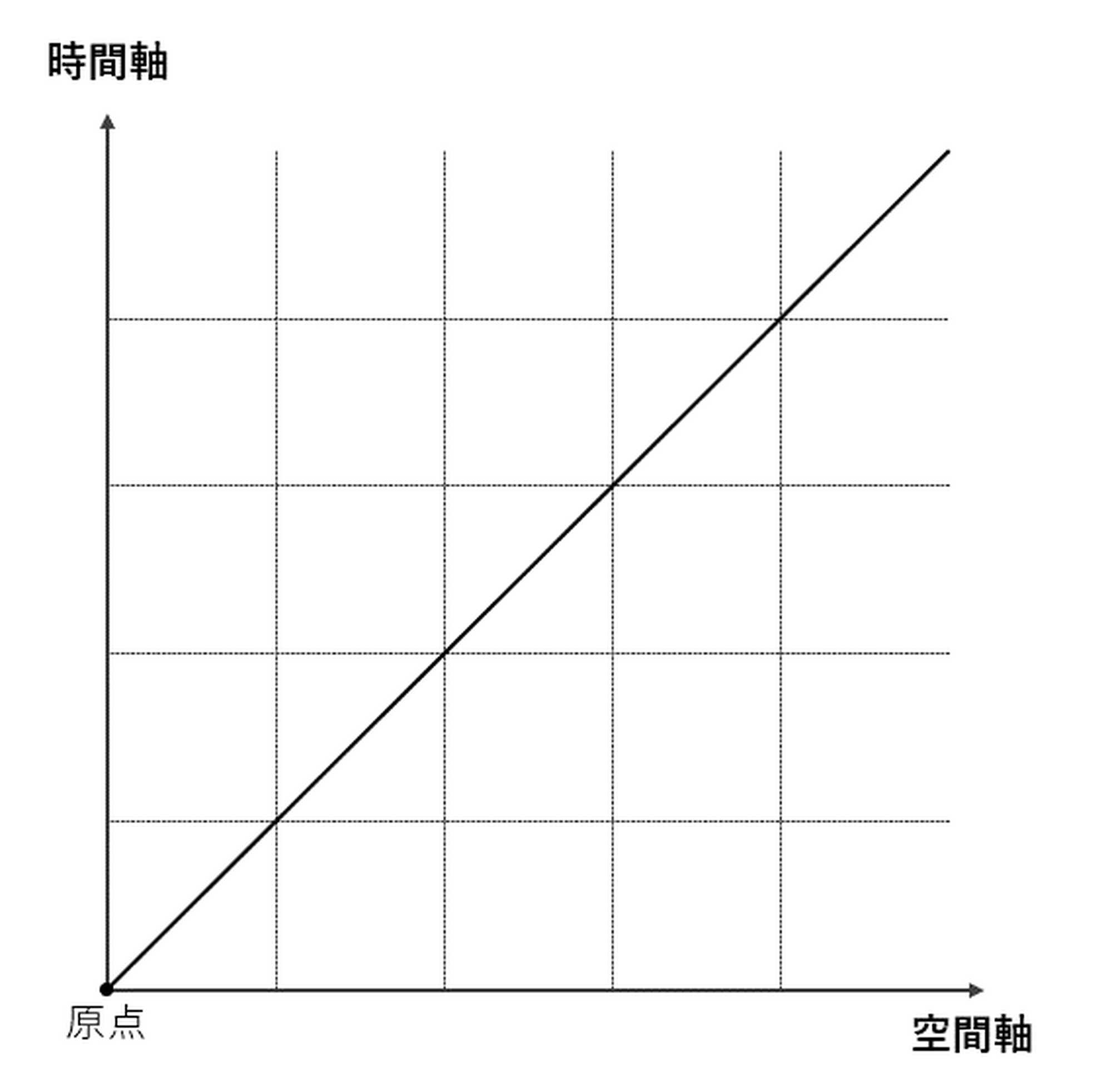
この運動を表す線分は[図2]では傾きがありますが、もしもニュートンが想定した不変不動な「絶対空間」も、全宇宙を一様に流れる「絶対時間」もないとしたら、この線分がまっすぐに立っているのか、それとも傾いているのかを判断することはできません。これはたとえば、天体も何もない無重力空間で、そこに浮かんでいる棒がまっすぐなのか斜めなのかと聞かれても答えられないのと同じです。
――上下を決める重力や座標軸のように基準になるものがないとわからないわけですね。
3次元空間のなかでどのように回転しても観測結果が変わらない物理現象(たとえば先述した磁石とコイルの実験)のことを「回転不変性がある」といいますが、ミンコフスキーはこれをある意味で拡張し、4次元時空(3次元空間+1次元時間)のなかでどういうふうに回転しても、この世界の見え方は変わらない。それこそが、相対性原理の意味だと主張しました。
――アインシュタインの発想を数学的に理論化したと。
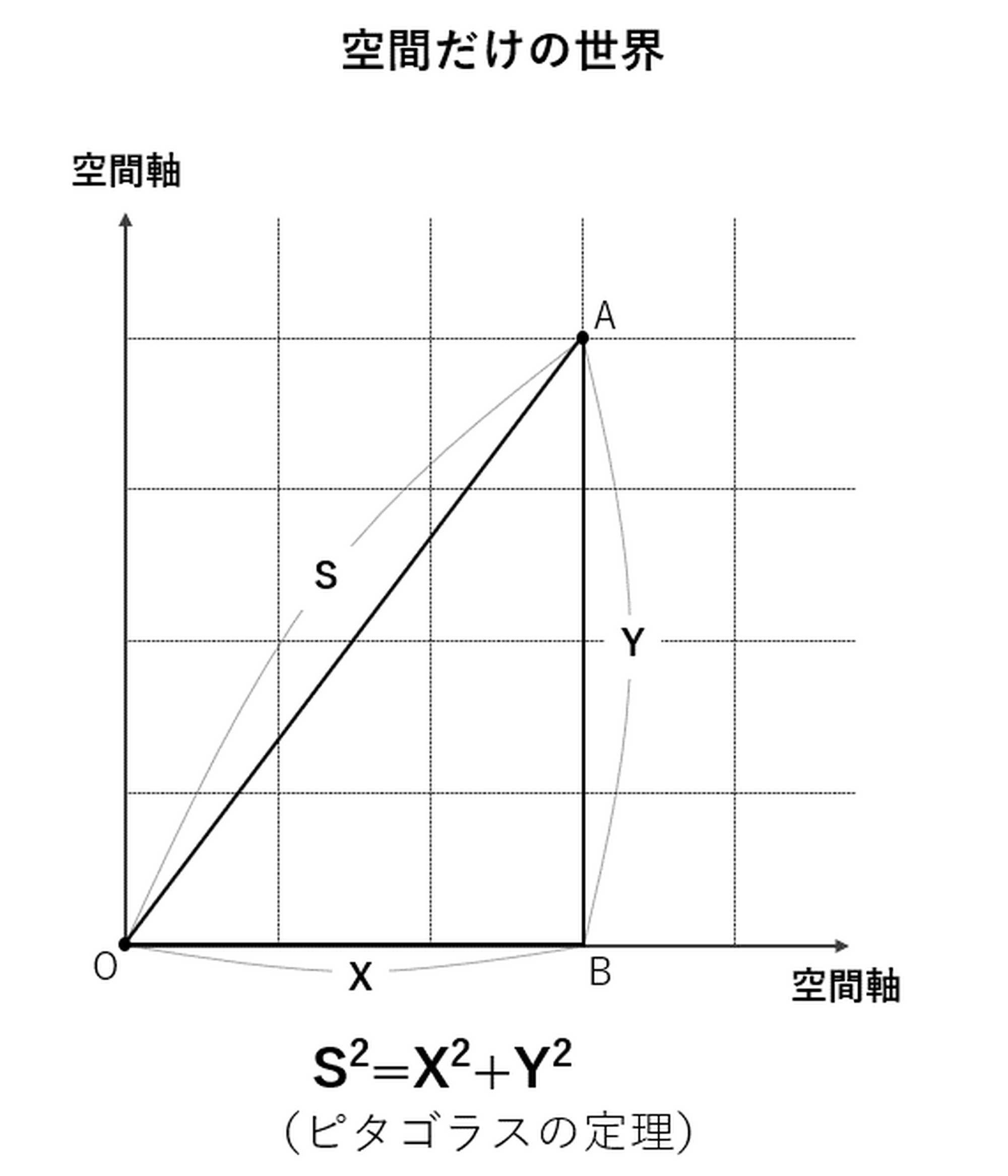
ただ、ここが重要なところなのですが、この4次元時空の幾何学は、3次元空間のそれとはちょっと違っているんです。たとえば3次元空間では、直角三角形の斜辺の2乗は直角をはさむ2辺の2乗の和になるという「ピタゴラスの定理」が成り立ちますが[図3-1]、時空の幾何学で同様に直角三角形を考えた場合、斜辺の2乗は時間方向の辺の長さの2乗と空間方向の辺の長さの2乗の差になるんです[図3-2]。
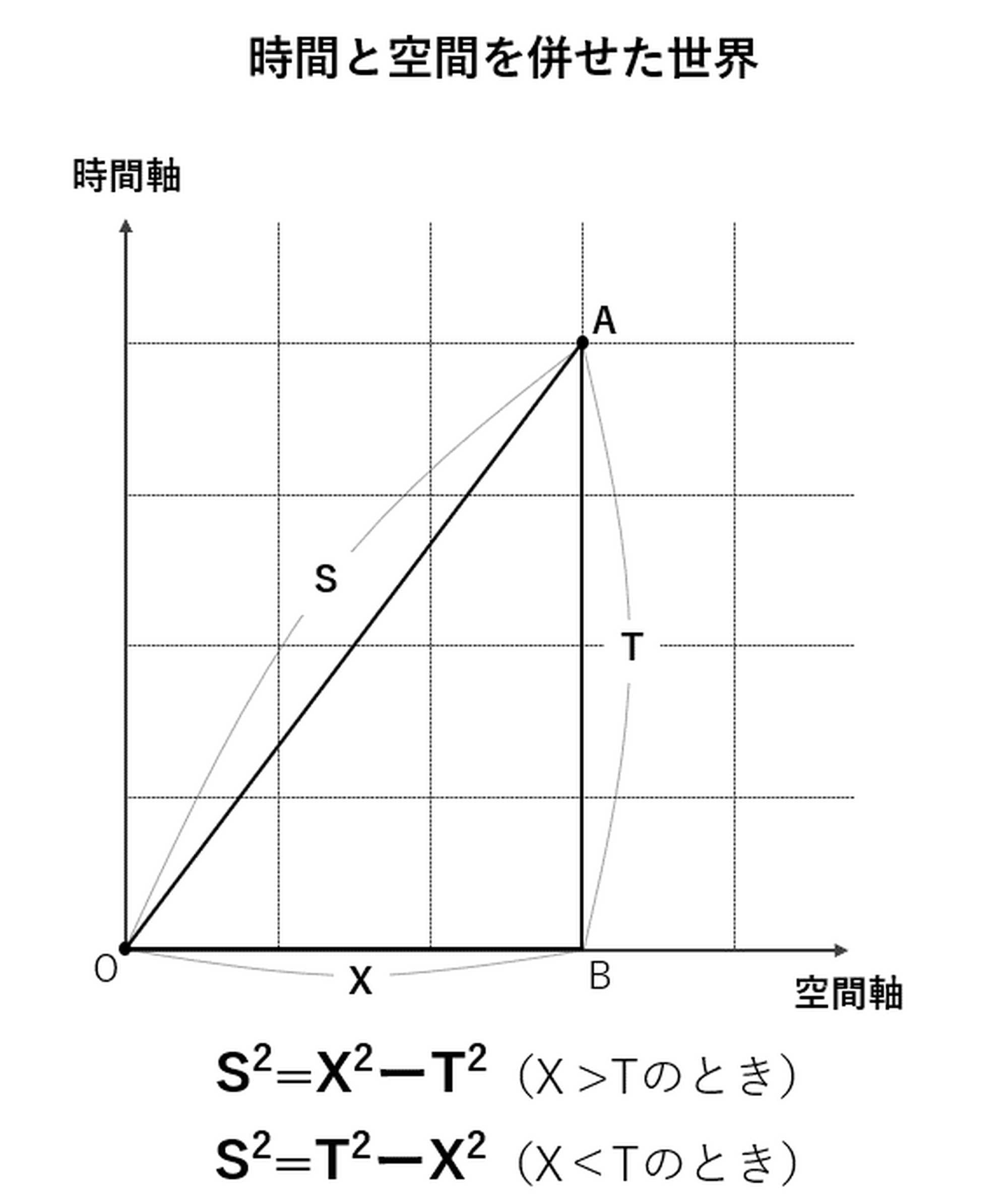
なぜそうなるかの説明はここでは省きますが、そのように幾何学を変更すると、4次元時空のなかでどれだけ回転しても物理現象は変化しない。すなわち、等速運動していることと静止していることの間に物理学的な違いはないという相対性原理が導かれることが明らかになったのです。


