――リンゴが木から落ちるのを見たニュートンが「リンゴは落ちてくるのに月はなぜ落ちてこないのか」と考えて万有引力の法則を発見したという話は、つくり話だそうですが面白いですよね。ニュートンは重力を「力」だと見なしたということでしたが、そこからどうやってすべての物は引き合うという発想に至ったのでしょうか。
前回も言ったように、ガリレオやニュートンの時代までは、物体が落下するのは物体そのものの性質だと考えられていました。もう少しくわしく言うと、物には宇宙の中心に向かう性質があると。当時は天動説ですから、すべての物体は宇宙の中心である地球のさらに中心に向かって落ちていくというわけです。ところが、いろいろな観測データから、どうやら動いているのは地球の方で、宇宙の中心は太陽だということがわかってくる。じゃあなぜ、地上の物体は真下に落ちていくのか。
――なんで太陽に行かないんだと。
そういったことを突き詰めていった結果、ニュートンは、重力を物体の性質ではなく力だと考えたわけです。「重力を力とみなす」というのは日本語だと変なのですが、gravityというのは「墓」を意味するgraveと語源が同じで、「重々しい」とか「深刻である」といったニュアンスの言葉です。つまり、下に沈み込んでいくのが物体の性質だという発想からきているのですが、ニュートンはそれを静力学で扱う力と同じものとして考えた。重力が力であれば作用・反作用の法則を満たすので、地球が月を引っ張って円運動させているように、月も地球を引っ張っているはずだと。そこからニュートンは潮の満ち引きが月の引力によるものであることを正しく洞察しています。
――月が地球の周りを回るのとリンゴが落ちるのがなぜ同じことになるのか、イマイチよくわかりません。
ニュートンは、塔の上から水平方向に物を投げ出したらどうなるかという思考実験をしています。塔の上から、ではリンゴにしましょうか、リンゴを水平方向に投げ出すと、投げ出す速度(=初速)が大きければ大きいほど、リンゴは塔から離れたところに落ちる。
ここで、地球は球体なので、投げ出す速度をうまい具合に調整すれば、リンゴが描く放物線と地球の表面の曲率(曲がり方の割合)が同じになり、リンゴは月と同じように地球の周りを回ることができるはずだ――ちなみに、空気抵抗がないとすると、リンゴを秒速7.9㎞で投げ出せば月と同じように地球を回り続ける計算になります――。そういうふうに考えを進めていったわけです。
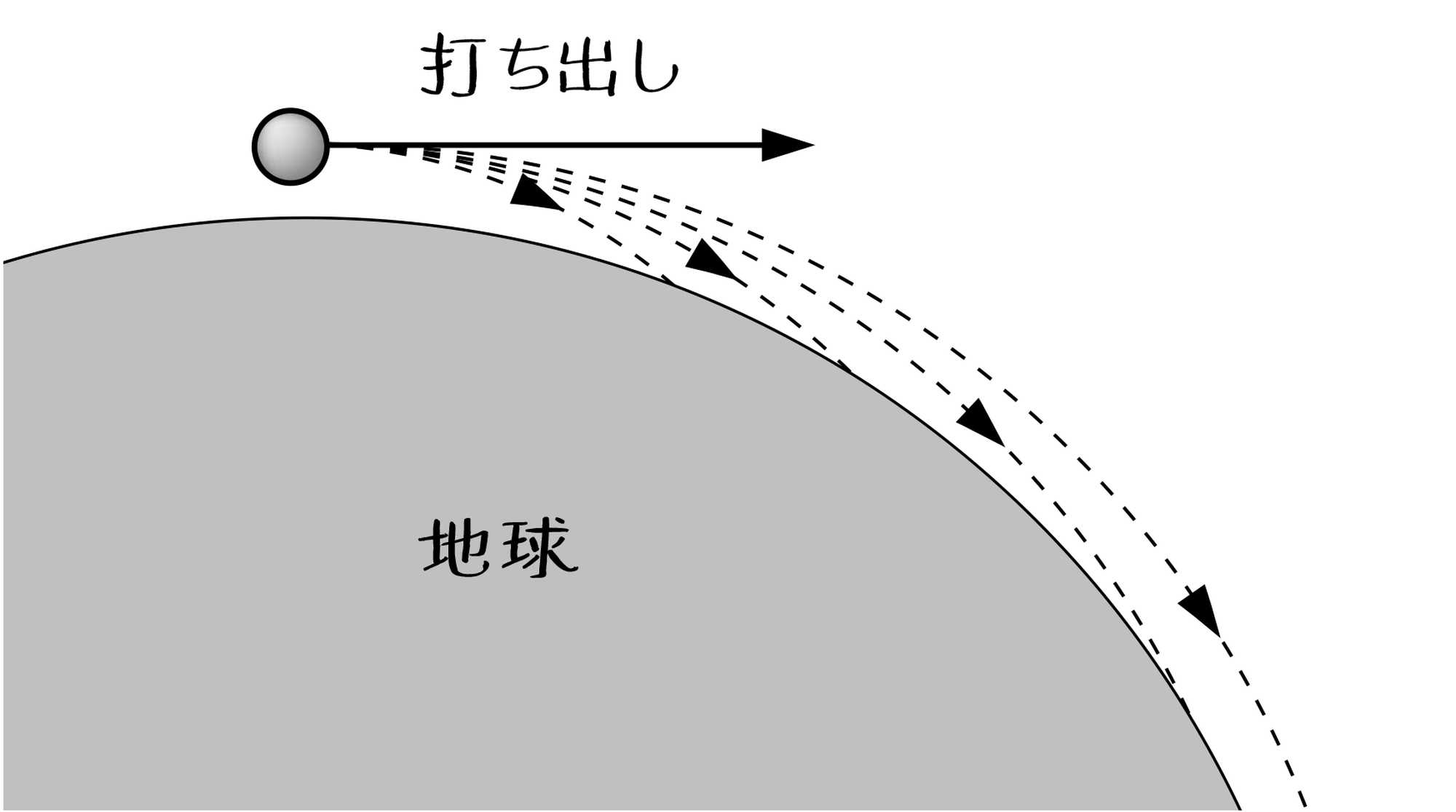
――なるほど! そういうことですか。つまり月は地球の球面に沿って「落ち続けている」から落ちてこないんですね。
そこから今度は、月に加わっている重力を考えていくことができます。リンゴと違って月は既に地球の周りを回っているので、その公転速度から遠心力を計算し、その遠心力が地球による重力と釣り合う(=向きが正反対で大きさが等しい)とすると、重力は重力源(この場合は地球の中心)からの距離の逆2乗(=2乗分の1)に比例するということがわかります。
これがいわゆる「万有引力の法則」ですが、当時の記録を見ると、ニュートンの計算は観測データと必ずしもぴったり一致しているわけではないんですね。観測誤差等があったせいで数値が合わず、ニュートンは何度も計算を繰り返したようですが、最終的にはある程度ちゃんとした理論体系を構築しています。
――それにしても、離れたところにある物体同士が引き合っているなんて、よく思いつきましたよね。
たとえば磁石や静電気のように、離れた物が力を及ぼし合う現象があるということは昔の人も知っていました。ただ、これらはあくまでも例外的なもので、不可思議な現象だと考えられていたようです。ニュートンが万有引力の法則をどのように発想したかというのはよくわかっていませんが、磁気や静電気から類推したということではなく、やはり洞察によって導いたのではないかと思います。
――物体の落下という地上の現象と、地球や月の公転運動という宇宙空間の現象が本質的に同じであり、同じ法則に従っていると考えたのがすごいなと思います。
そうですよね。実際、古代ギリシャでは、地上で成り立つ法則と月より遠方の天体の世界で成り立つ法則はぜんぜん別だとされていました。地上ではいろいろと複雑な現象が起きるけど、天体の世界は幾何学に支配されていて、物体はすべて円運動をしていると。それを否定し、あらゆるところで成り立つ法則があるというふうに考えを広げていったのは、ニュートンをはじめとした当時の科学者の功績だと思います。
重力にまつわる2つの謎
――ガリレオがピサの斜塔から木でできた球と鉄でできた球を同時に落とし、物体の落下速度が重さによらないことを証明したという話がありますが、これもつくり話だそうですね。
その話はガリレオの死後何十年もたってからできたものですが、木や石や金属といった材質が異なる物質を同時に落とし、どれが先に落ちるかという実験をした人はガリレオより前に実在します。しかもその話は、ガリレオの著した『新科学対話』に出てくるんです。で、その実験の結果はというと、大体は金属が先に落ちるんですよ。
――え、そうなんですか?
密度の大きい物体の方が空気抵抗が小さいので先に落ちるんです。ガリレオは自分の著書にそのことを書いているくらいですので、もしもピサの斜塔でそんな実験をしたら「重い物は軽い物より先に落ちる」というアリストテレスの説を擁護してしまうことになる。
ガリレオが実際にやったのは、前回も言いましたが、斜面の角度をいろいろ変えて、そこを転がる球の速度がどのように変化するかを調べる実験です。その際に、斜面の摩擦をなるべく小さくしたり、転がす球を真球に近づけたりといったいろいろな工夫をして、ようやく、落下する物体が等加速度運動をするという法則を導きました。根本的な法則を導く際に、実験データをかく乱する要素を取り除くのがいかに難しいかということをガリレオは身に染みてわかっていたはずです。それなのに、ピサの斜塔から球を落とすといった雑な実験するわけがないんです。
――ピサの斜塔で実験したことになってるとガリレオが知ったら怒りそうですね。
ガリレオは、世界の本質は簡単な数式で書かれるはずだという確信を持っていました。それを受け継いだのがニュートンで、だからこそ彼は重力が逆2乗に比例するという単純な法則を導くことができたわけです。
ところがこのニュートンの理論には二つの問題がありました。一つは、重力がなぜ物体の質量に比例するかということです。ニュートンはガリレオの実験結果を説明する際に、重力が物体の質量と比例関係にあると仮定しているのですが、なぜそうなるのかには一切触れていません。彼の主著の『プリンキピア』は非常に論理的に書かれているのですが、所々でこのようにしれっと、ただの仮説に過ぎないことが紛れ込んでいるんです――時間や空間の定義もさらっと流されています――。いろいろ考えたけど、どうしてもわからなかったのでしょう。
もう一つは、前にもすこし触れましたが、重力がなぜ何もないところを伝わるのかという問題。力が真空を伝わるというのはどうしてもわかりづらいんですよね。それで、レオンハルト・オイラー(1707-1783)をはじめ、多くの科学者が重力を伝える媒質があると考えて理論を組み立てようとしたけど、結局はどれもうまくいきませんでした。
この二つの問題をいっぺんに解決したのが、20世紀初頭に登場したアインシュタインの一般相対性理論なわけです。


